¿CÓMO SE SIGUEN LAS RUTAS EN EL AIRE?

La navegación es un asunto interesante: se hace tomando una carta de navegación, que no es otra cosa que un mapa especial para navegar, y planeando si voy a viajar de A a B, por dónde lo voy a hacer y a cuál altitud, por cuáles pueblos o ciudades voy a pasar para chequear la precisión de mi ruta y con cuáles detalles debo estar alerta en el terreno. Eso es navegación visual, muy útil en tramos cortos, pero limitada, por la visibilidad, a las horas diurnas; y la navegación por instrumentos de vuelo que nos exige conocimientos precisos y es útil para largas distancias y  rutas en las cuáles no hay puntos de referencia, por ejemplo, el mar.

.

Un problema fascinante de la navegación de grandes distancias es la geometría involucrada en ella. Todos conocemos los mapas escolares, muy coloridos y bonitos; tienen toda la información que le interesa a los estudiantes: la forma de los continentes y los paises, las montañas, las carreteras etc. Pero no serían útiles para volar pues carecen de datos indispensables, cómo la manera como debemos seguir la ruta y las alturas a las que deberíamos hacerlo.

.

Los pilotos siguen las rutas por medio de rumbos  que pueden seguir gracias a sus brújulas, las cuáles muestran en cual dirección exacta están localizados los polos magnéticos. Si sabemos dónde está el norte magnético podemos ponerlo a un determinado ángulo con respecto de nuestra ruta: si lo ponemos a nuestra izquierda a noventa grados de la dirección en la cuál viajaremos, es seguro que vamos hacia oriente, es decir, en una brújula de boy scout el norte nos quedaría a la izquierda, iríamos con un rumbo de noventa grados. Fácil ¿no?. Del mismo modo podemos viajar hacia otros 359 rumbos diferentes con la ayuda de la brújula, solamente poniendo el norte a la izquierda o hacia cualquiera otro rumbo deseado. Esto es muy útil en pequeñas áreas.

.

Pero en grandes áreas la cosa  funciona  a medias si se hace de ese modo. Pues a pequeña escala la tierra es aceptablemente plana, y la geometría plana es suficiente; otra cosa pasa cuando tomamos pedazos más amplios del planeta, y la superficie deja de parecer plana para volverse una compleja superficie esférica. Ahí ,las cosas se van poniendo complicadas.

.

Sabemos que la distancia más corta entre dos puntos es la recta. En la geometría plana eso es irrefutable; en nuestro mundo plano de calles cuadriculadas no tiene discusión y quien se atreva a discutirlo pasará fácilmente por la puerta de la clínica psiquiátrica. Pero si ampliamos nuestro territorio más allá, la superficie de la tierra comienza a curvarse hasta que llegamos  hasta una nueva dimensión. La geometría  falló escandalosamente. Ella  dice que un viaje recto que inicia en un punto se extiende hasta el infinito, pero en este otro escenario volvimos al punto de partida, al darla vuelta al planeta.

.

La falla es culpa de la esfericidad de la tierra. Lo que ocurre es que  en nuestra pequeña escala humana la tierra es aceptablemente plana; no pasa de ser un asunto académico que en nuestra vida diaria no nos afecta: en un área pequeña podemos tomar una línea recta entre A y B y llegaremos más rápido que describiendo una curva.

.

Pero en un área mayor, digamos, un vuelo transatlántico ya eso se vuelve falso, y si la distancia a recorrer aumenta, más falso.

.

La geometría reconoce en la esfera dos tipos de círculos: los círculos máximos y los mínimos. Los Círculos máximos tienen la misma circunferencia del ecuador, despreciando el poco achatamiento de la tierra en los polos; y lo mínimos son más pequeños y tienen cualquier circunferencia menor que la del ecuador. Basta tomar una naranja y cortarla en cascos: cada corte es un círculo máximo. Pero si tomamos otra naranja y le hacemos un solo corte diagonal obtenemos un circulito menor. 

.

Resulta que para solucionar esta aparente anomalía existe la cartografía: la ciencia y técnica de la elaboración de mapas que se basa en matemáticas precisas y especializadas que no están al alcance de la enseñanza escolar.  Conocemos el mapamundi, esfera rodeada con una maya de líneas, unas paralelas que, como su nombre lo indica, son paralelas, paralelas al ecuador terrestre; y otras llamadas meridianos que van de polo a polo y se cruzan en esos puntos, y sólo son paralelas sobre el ecuador, en ninguna otra parte.

.

Para facilitar el cálculo de rutas y distancias se elaboran las cartas como proyecciones de estas líneas sobre una superficie plana, y el resultado es  como si desolláramos al planeta y extendiéramos su piel sobre una  mesa. Tenemos tres tipos de proyecciones: la cónica, la cilíndrica y la polar.

.

Las proyecciones son como si colocáramos un poderoso foco de luz dentro de la tierra, tal como si ella fuera de vidrio, y luego proyectáramos una diapositiva esférica, del planeta, sobre superficies planas. Hace falta algo de  imaginación para entenderlo. Todos sabemos que tal cosa no es posible en la realidad, así que estas proyecciones en realidad se logran con aplicación de matemáticas, pero no por eso no son exactas.

.

La proyección cónica supone que tomamos un gigantesco cono de papel fotográfico y  situamos al planeta dentro de él, con su lamparita encendida, y luego revelamos la fotografía; pero para poder extenderla sobre la superficie plana la cortamos desde el vértice hasta el borde siguiendo un meridiano. El resultado será una serie de líneas rectas que se separan hacia el ecuador, se acercan hacia el polo, y se cruzan en alguna parte fuera del papel, los paralelos son arcos concéntricos cuyo centro se encontaría en el polo. Los continentes sufren una gran deformación: se comprimen cerca de los polos y se amplían cerca del ecuador. Esta carta no conserva la relación de área, quiere decir esto que  un país puede verse comparativamente más grande o más pequeño de lo que sería en realidad, de modo que si queremos conocer si una nación tiene más o menos área que otro no podemos confiar en esta proyección.

.

La proyección cilíndrica es como poner el globo terráqueo dentro de un gran cilindro. su proyección resulta en una red de líneas, que forman rectángulos, los cercanos al ecuador son cuadrados perfectos pero se estiran en rectángulos cada vez que nos alejamos un poco del ecuador. Sólo los paises cercanos al ecuador conservan su forma original, pero a medida que se alejan hacia el polo se estiran notoriamente,así pues sólo podríamos comparar en tamaño, con alguna veracidad, a los países que se encuentran cerca del ecuador, los demás se verán mucho más grandes de lo que en realidad son.

.

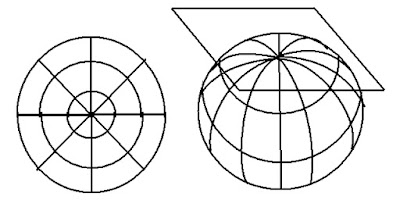
La proyección polar es como poner el papel fotográfico sobre el polo, de modo  perpendicular al eje que va de un polo al otro. El resultado se ve como varios círculos concéntricos cruzados por los meridianos, que son líneas rectas que salen radialmente desde un punto central que coincide con los polos. Puede decirse que el terreno  no sufre deformación en el centro de esta proyección, pero ssí al alejarse de él, y mucha.
.

 

Cada carta de navegación tiene un propósito especial. Por ejemplo la proyección cónica es útil para vuelos de larga distancia, pues permite seguir rutas más cortas entre dos puntos muy lejanos, siguiendo diferentes rumbos: el piloto debe hacer ajustes periódicos a su rumbo para seguir una línea aproximadamente curva sobre el globo terrestre; en cambio la proyección cilíndrica le permite trazar rutas con rumbos fijos, tales que desde un punto hacia otro vuela un solo rumbo y es útil para vuelos cortos. Con ambas cartas de navegación puede llegar a su destino con precisión, todo depende de la longitud del vuelo proyectado.
.
Esto se debe a que en razón de la curvatura de la tierra, para vuelos cortos se puede considerar que una trayectoria rectilínea es suficientemente económica, pues la esfericidad del globo tiene una influencia despreciable; sin embargo en vuelos de largo alcance la variación de rumbos permite ajustarse a un círculo máximo terrestre que minimiza la duración del vuelo, y eso se refleja en la economía de combustible. 
.

Para dar una idea de qué es un círculo máximo citaré el ecuador, que es uno de ellos, pero no es el único, también lo son los meridianos y cualquiera otro que divida el globo en dos mitades, y que teóricamente incluye al centro de la tierra en su plano. Cualquiera otro es un círculo menor, llamado así porque su diámetro es inferior al del ecuador. y su plano no incluye al centro de la tierra. Todo esto si nos atrevemos a considerar a nuestro planeta como una esfera perfecta, despreciando el achatamiento en los polos, el cual en la navegación tiene muy poca influencia.
.
Cualquier par de puntos localizados en un círculo máximo están situados dentro de una línea directa que garantiza que esa distancia es la menor, no pasando lo mismo con los que se sitúen en un circulo menor.

En la esfera de alambres  he trazado dos rutas y también en la proyección cónica a la derecha. La línea roja se mueve de esquina a esquina en las cuadrículas,tiene un rumbo constante de 45°. Pero la línea azul cruza todas las cuadrículas con distintos ángulos respecto de las tangentes de  los meridianos en la esfera, y de las rectas en la proyección cónica. En ambas figuras es posible observar, al menos intuitivamente que la línea azul es más corta.
.
Ya teniendo una ruta adecuada en el plan de vuelo, el piloto se puede guiar por instrumentos de vuelo que le indican su posición respecto a un punto, o más, conocidos sobre la superficie terrestre y registrados en su carta de navegación. de manera que constantemente se puede conocer la situación exacta. 
.
Es pertinente anotar que cada vez se popularizan más los sistemas de navegación global o GPS, mediante los cuáles el avión calcula constantemente su posición actualizada y la muestra en una pantalla, y el piloto puede determinar su distancia, velocidad y desviaciones respecto de la ruta, además del viento que puede estar afectando su  trayectoria; y el uso de sistemas de navegación automática que llevan a la aeronave hasta su destino, y algunos aún pueden aterrizar al aeroplano, con una mínima intervención humana, y por lo tanto con una mínima posibilidad de errores de navegación.